Forum Replies Created
-
AuthorPosts
-
-
at 18:30 #30351
Bella
ParticipantWhy is no perfect square a multiple of 3n+2?
The statement= n^2= x(3n+2). Where x is any number from 1-below infinity. (I will not count infinity as a solution since technically infinity does not have a numerical perfect square)
This is because no number squared can give 3n+2. If you try 1 and plug it into the function, it will give you 3+2 = 5. If you try 2, it will give you 8. 4 is not a multiple of 8. Using higher prime numbers: 123^2= 15129 plugged into 3n+2 = 371. 15129/371=40.7789757412. (Most equations use a calculator (hope you dont mind)). Also, using the largest 5 digit prime number = 99991. 99991^2=9998200081. plugged into 3n+2=299975 9998200081/299975=33330.1111126. Which is not a whole number.
After plotting into desmos, we can only see ONLY 2 points, (0,0) and (-0.889, -1.333). Using a calculator, we can calculate that the slope is 3.0002001133476 which is unfortunately is not a whole number. This means that no matter what you input as n, you will never get a whole number.
(I have no idea if this is right. Just a stab in the dark)
-
at 08:58 #23750
Bella
ParticipantMy homework:
Paragraph:
All around the world city streets exploded with people, cars skidded into each other as the noise fell on them and then rolled off like a tidal wave over hills and valleys, deserts and oceans , seeming to flatten everything it hit.
My thought:
What I think makes this paragraph frightening is that how sudden city streets exploded along with all those people that died and the funny thing is that the author seems to be saying all this in a particularly calm way. And also, the interesting part is the author is using a language that is amazing and what makes it more action-packed like how the noise fell on the cars that skidded into each other.
-
at 04:20 #11438
Bella
Participant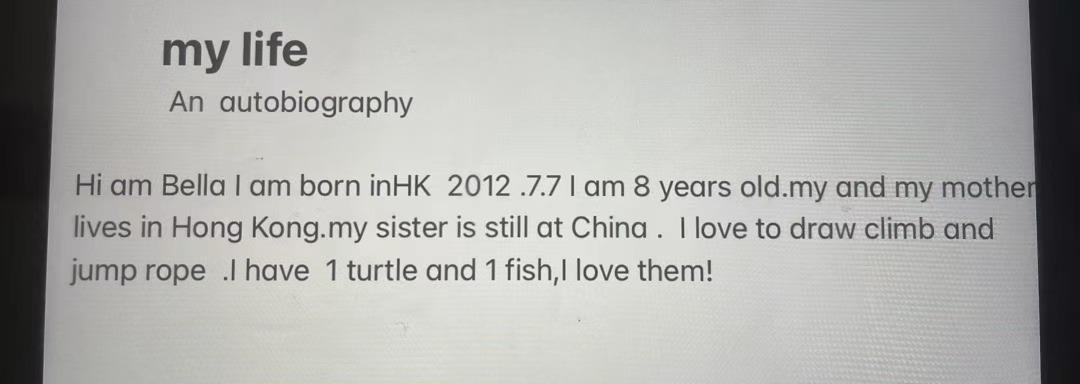
-
at 04:13 #11436
Bella
Participant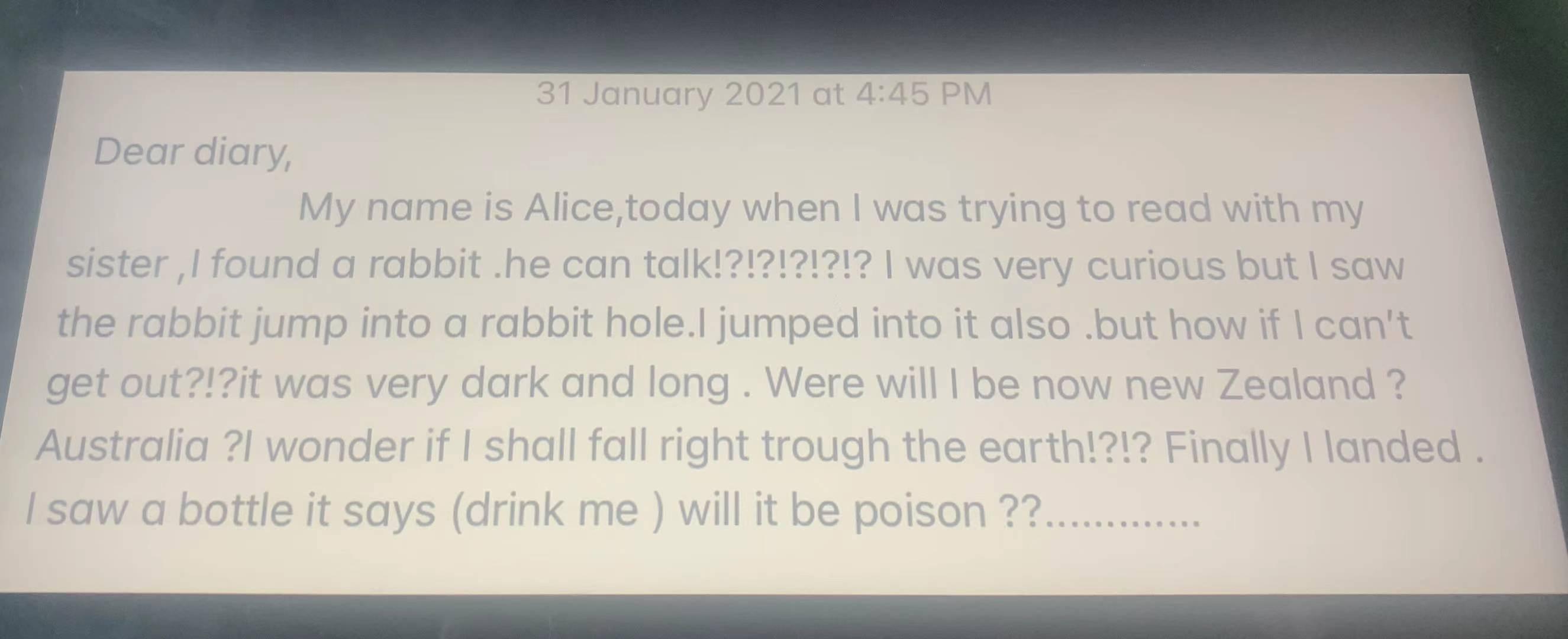
-
-
AuthorPosts
