- This topic has 12 replies, 5 voices, and was last updated April 25, 2023 by
.
-
Posts
-
-
-
-
Attached are the week 2 slides. If you are reading this before taking our week 2 class in the Saturday Feb 18th class, I would recommend not reading the contents until we have the session. Again, these are just for your own review, as we had some much more challenging problems this week so it may be beneficial to go over them on your own time. See you next week and feel free to ask any questions on here if you have them.
-
Hello all, I have a slight correction on one of the questions covered in today’s class. A screenshot of the question is included below.
In class I mentioned that 1, 2, 3, and 5 could all be congruent. This is still true, but I should have been more careful and explained that 2 and 3 must be congruent, as well as 5 for reasons a bit out of scope for our current level, but 1 doesn’t have to be. There are 2 different ways to draw the triangle from the information given in 1, one of which is congruent and the other is not. Of course, the case that isn’t congruent looks drastically different from the image shown in the question, but because these drawings aren’t to scale it could technically not be congruent. A revised answer would be 2,3, 5, though the pair of 2,3 is the answer we were mainly looking for (which most of you got anyways).
We will be discussing congruency in depth next week so I will make this case more clear if any are confused. Have a wonderful week.
-
-
-
-
Why is no perfect square a multiple of 3n+2?
The statement= n^2= x(3n+2). Where x is any number from 1-below infinity. (I will not count infinity as a solution since technically infinity does not have a numerical perfect square)
This is because no number squared can give 3n+2. If you try 1 and plug it into the function, it will give you 3+2 = 5. If you try 2, it will give you 8. 4 is not a multiple of 8. Using higher prime numbers: 123^2= 15129 plugged into 3n+2 = 371. 15129/371=40.7789757412. (Most equations use a calculator (hope you dont mind)). Also, using the largest 5 digit prime number = 99991. 99991^2=9998200081. plugged into 3n+2=299975 9998200081/299975=33330.1111126. Which is not a whole number.
After plotting into desmos, we can only see ONLY 2 points, (0,0) and (-0.889, -1.333). Using a calculator, we can calculate that the slope is 3.0002001133476 which is unfortunately is not a whole number. This means that no matter what you input as n, you will never get a whole number.
(I have no idea if this is right. Just a stab in the dark)
-
Attached are the slides used in our week 6 class. As usual, there is no homework, but there is an optional challenge problem like last week. It is as follows:
Why is there no perfect square of the form 3n+2, where n is an integer?
In other words, why are all perfect squares multiples of 3, or multiples of 3 plus one. Try to come up with the best proof you can.
-
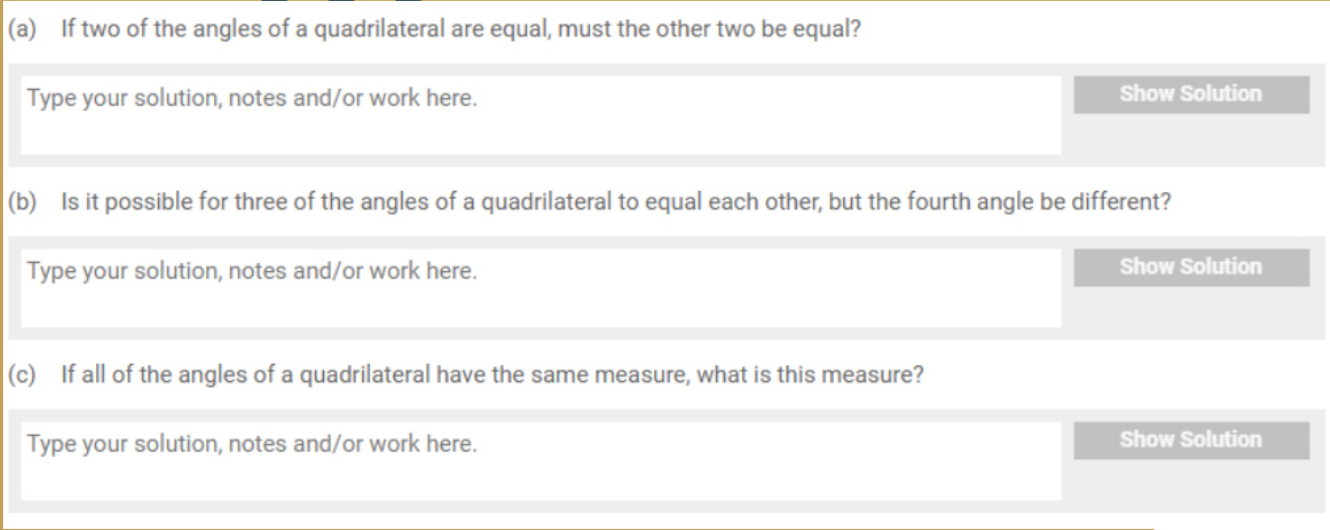
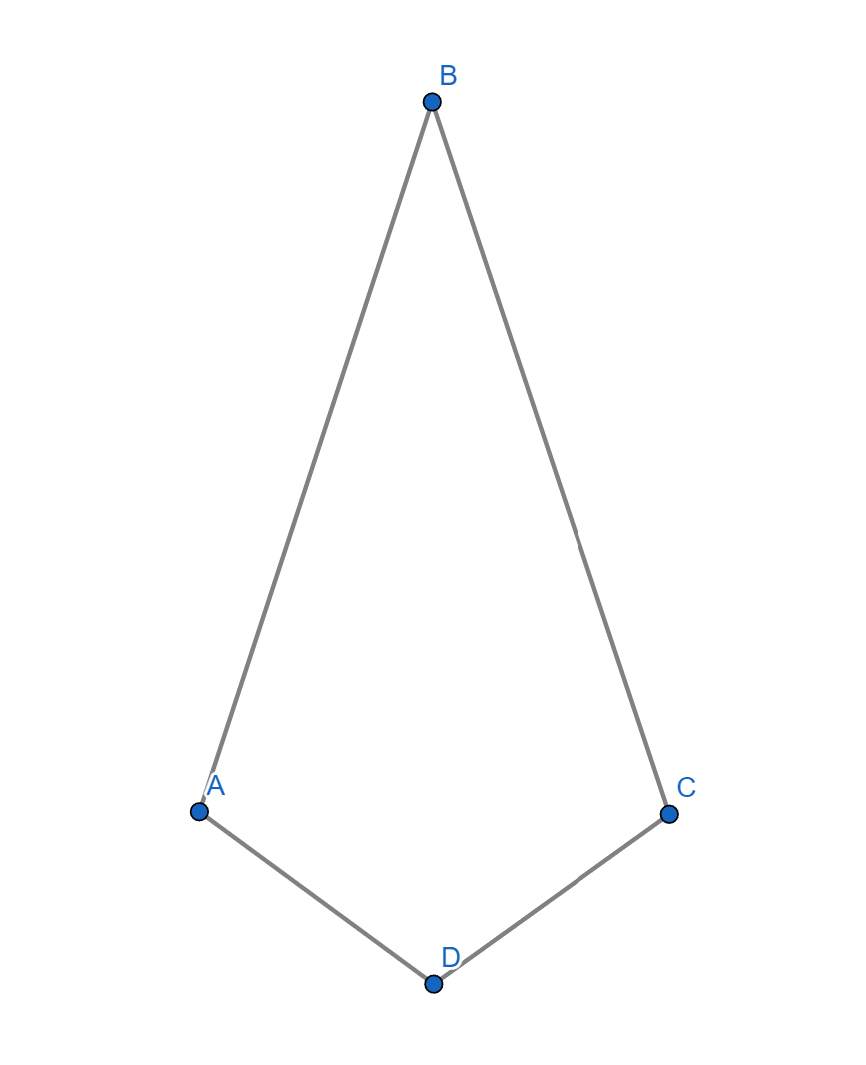
Attached are the slides used in our week 8 clas. I want to clear something up surrounding the question on slide 6 – also listed below. What the question was asking in part b) I fear was not clearly explained and I wasn’t able to accurately draw an example to scale on zoom that proved the answer to B) is yes, but I took the time after class to make this correctly. If you don’t believe the answer is yes, feel free to take a protractor to my solution. So – to reiterate, the answers to a), b), and c) respectively are No, Yes, and 90 degrees. If you’re watching this lesson’s recording, I recommend skipping this part as it may be confusing to have somewhat contradictory answers. Thanks, and have a wonderful break everyone. See you soon.
Question:
-
-
-
-
- You must be logged in to reply to this topic.